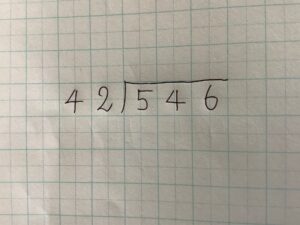割り算　筆算のやり方　計算が苦手な小4の対策

計算が苦手な息子の割り算について書いた記事です。

実際に息子がつまづいたポイントや教え方、取り組み方を書いていきます。

管理人と息子は割り算筆算をマスターするまで遠回りをしたので、スムーズに学習できるようにポイントを抑えながら解説していきます。

教科書通りに学習しては効率が悪い

学校の授業では割る数が１桁の筆算を終了後、しばらく間が空いて割る数が2桁の筆算を学習していきます。

特に問題ないように思いますが、逆に、何故、割る数1桁と2桁を間隔をあけるのかわかりません。

実は息子が学習している時に、ある問題が発覚しました。

割る数が1桁の筆算、割る数が2桁の筆算を単元ごとにごとに学習している時は問題ありませんでした。

しかし、割る数が1桁・割る数が2桁、割られる数が2桁・割られる数が3桁などをランダムに組み合わせた筆算問題をやってみると間違いだらけだったのです。

「商を立てる位置」やら、「たてる・かける・引く・おろす」の順番がめちゃくちゃになったり大混乱でした。

単元学習だと何も考えず（理解せず）、学習した同じパターンで筆算をしていたのでしょうが、ランダムに出題されると本当に理解しているのかがはっきりわかります。

家で学習する時は、割る数が１桁・２桁、割られる数が2桁・3桁の筆算は一気に学習することを強くおすすめします。

商のスタート位置がいいかげん

わり算ひっ算のつまずき第一歩が商のたてる位置（スタート位置）の決定です

わり算の筆算を学習する上で、商のたてる位置（スタート位置）をどこにするのかをしっかり理解しなければ色々なわり算が出題された時に混乱します。

具体的には「284÷3」なら商は8の上にたてなければいけません。「424÷3」であれば商は4の上にたてなければいけません。

しかし、子供はどこに商をたてればいいのか混乱してしまうケースがあります。

2桁÷1桁の単元学習だけをしていると商は2番目に書いておけばいいと思い込んでおり、特に商をたてる位置を考えていませんでした。

大人にとっては簡単なことでも子供にとっては初めてのことで難しく感じます。

このつまずきポイントをうまく乗り切りことで自分は「計算が得意だ！」。「算数が得意だ」になってくれれば儲けものです。

商をたてる位置がわからないという問題を簡単に解決できた息子が取りんだ方法を説明していきます。

用意するものは消しゴムです。

割られる数を消しゴムで隠しながら商をたてる位置を決めていきます。

例題で見ていきましょう。

①消しゴムで割られる数の546のうち46を隠します。

②上記のように5÷42だけ見えるので、5÷42はわれないので消しゴムをスライドさせます。

③上記のように割られる数は54だけ見えるので54÷42となります。54÷42は割れるので商をたてる位置が4の上と決定します。

➄商の立てる位置が決定したので実際に商をたててみます。54÷42は商１を4の上にたてることができます。

このように割られる数546を消しゴムで隠し、1桁ずつ右にスライドし「割れる？」「割れない？」と判断していけば商をたてる位置を間違えることはなくなります。

桁が大きくなっても同じことです。

たてる・かける・ひく・おろすの徹底

前の項目で商をたてる位置を決定したので、今度は実際にわり算ひっ算をやっていきます。

ひっ算が苦手な場合、リズムで計算していくとスムーズになります。

息子が実際にやってみた方法をあげていきます。

息子は童謡「10人のインデアン」の歌にのせるとスムーズにできました。

「ひーとり、ふーたり、３にん、４にん」を替え歌にします。

「たーてる、かーける、ひーく、おろす」にするとしっくりいきます。

リズムよく歌にのせるのは、非常に効果的なので是非試してみてください。

この10人のインデアンの歌にのせる方法は東進オンライン学校の先生が教えてくれた技です。

割り算筆算　あまりの数の大きさに注意

あまりの数が割る数より小さければ正解の可能性が高いです。

しかし、あまりの数が割る数より大きい数になった場合は絶対に不正解です。そのことに全く気付かずやり終えたことに満足しているお子さんは要注意です。

最後まで気を抜かず割る数がより大きい数が出てきたら、「あっ、これはどこかで計算間違いしているぞ」とすぐに気づかなければなりません。

計算ミスはどうしても出ますが、どこでミスをしたか気づけるかが「できる子」と「できない子」の違いです。

考えなくてもスラスラできるようにする

わり算ひっ算は文章問題などを解く過程で当たり前のように使えるようにならなければいけません。

スムーズに解けるようになるまではランダム問題を何回も繰り返し学習していきます。

初めはゆっくり商を立てる位置などを確認しながら学習していくことが重要です。

何度もランダム問題の演習を重ね、タイムも意識しながら解けるようにすることも重要です。

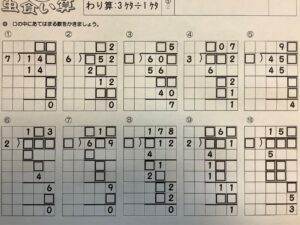
割り算筆算虫食い問題までできるように！

 3桁÷1桁の虫食い問題までスムーズにできるようにしたいです。

最近は学校のカラーテストでも虫食い算が出題されるので、この辺りはしっかりおさせるべき標準レベルの内容となります。

虫食い問題というとアレルギー反応のように拒絶するお子さんも多いと思いますが、虫食い問題は筆算の理解度を計るのにも最適です。

割り算筆算のランダム問題がスムーズにできるようになっていれば、現状は相当な計算力がついているはずです。

更にレベルアップをはかり、何より子供自身が「割り算の筆算ならまかせろ！」というくらい自信がもてるようになります。

虫食い問題は考えなければできないので確かに難しいです。

しかし、じっくり考える時間も必要なので是非チャレンジしてもらいたいです。

「筆算工房こつこつ」というサイトがとても充実していますので活用してみてください。

4年生　割り算筆算のまとめ

息子はたし算・ひき算・かけ算・わり算すべての筆算の学習でつまずきました。

割り算の学習前もつまずくことは覚悟していたので特別驚きはないです。

いつものようにコツを学習した後はひたすら演習を繰り返すのみです。

これまでもそのようにして乗り越えてきました。割り算のひっ算もこれで乗り越えることあできたので、もし、割り算筆算でつまずいているお子さんがいれば、わかるまでじっくりトコトン付き合ってください。

算数の学習の基礎力はやはり計算力です。四則計算は筆算をスムーズにできるようにし、最終的にはある程度暗算でできるようにしたいです（中学校にあがるまでには）。